树状数组

当我们涉及到求前缀和的情况下，我们很容易想到求前缀和数组，然后以O(1)的时间复杂度求出某一区间的元素之和。但是如果我们修改了数组中某一个点，那么我们就需要O(n)的情况下来维护前缀和数组。如果涉及到了需要修改数据并且查询区间和的需求，我们的前缀和算法涉及到的时间复杂度就是O(n^2)，这个时候我们引入树状数组来解决问题，树状数组就是借鉴了前缀和的思想，将维护从O(n)下降到O(logn)，将查询从O(1)上升到O(logn)，那么最后的时间复杂度就是O(nlogn)。这是一个相对来说比较平衡的方法。说白了就是单点修改，区间查询。

前置概念

树状数组主要是参考的二进制优化和前缀和的思想，如果我们需要求数组前1-n个元素的和，我们可以将这些分成一部分一部分。每一部分都记作C数组。这个数组在树状数组中是以树状来表示的。现在听起来可能很抽象，可以带着疑问往后看。n可以表示为二进制，如下：

$$n = 2^{x_1} \times 2^{x_2} \times 2^{x_3} \times …\times 2^{x_{k-1}} \times 2^{x_k} (x_1 > x_2 > x_3 > .. > x_{k-1} > x_k)$$

形象看起来就是n的二进制表示：

$$n = (1001…10101)_2$$

这样子，我们的n就可以变成：

$$n = (1000…00000 + 0001…00000 + … +0000…10000 + 0000…00100 + 0000…00001)_2$$

抽象出来，我们总结一下我们想求1- n元素之和，并且n的表达式为上面所述，那么我们可以分解成为：
$$
\begin{cases}
sum\bigl(n - 2^{x_k},n\bigr] (len = 2^{x_k})\
sum\bigl(n - 2^{x_k} - 2^{x_{k-1}},x - 2^{x_k}\bigr] (len = 2^{x_{k-1}})\
…\
sum\bigl(n - 2^{x_k} - 2^{x_{k-1}} - … - 2^{x_3},x - 2^{x_k} - 2^{x_{k-1}} - … - 2^x_4\bigr] (len = 2^{x_3})\
sum\bigl(n - 2^{x_k} - 2^{x_{k-1}} - … - 2^{x_3} - 2^{x_2},x - 2^{x_k} - 2^{x_{k-1}} - … - 2^{x_4} - 2^{x_3}\bigr] (len = 2^{x_2})\
sum\bigl(n - 2^{x_k} - 2^{x_{k-1}} - … - 2^{x_3} - 2^{x_2} - 2^{x_1},x - 2^{x_{k-1}} - … - 2^{x_4} - 2^{x_3} - 2^{x_2}\bigr] (len = 2^{x_1})
\end{cases}
$$

其中sum表示求范围内的数组下标对应元素之和，我们可以将sum表示成c数组，我们可以总结出来:

$$c[x] = \bigl(x - lowbit(x),x\bigr] (len = lowbit(x))$$

修改更新与查询

我们上一节总结了c数组的概念，我们现在可以总结一下c数组的规律，首先我们先画出所有1-16的c数组。

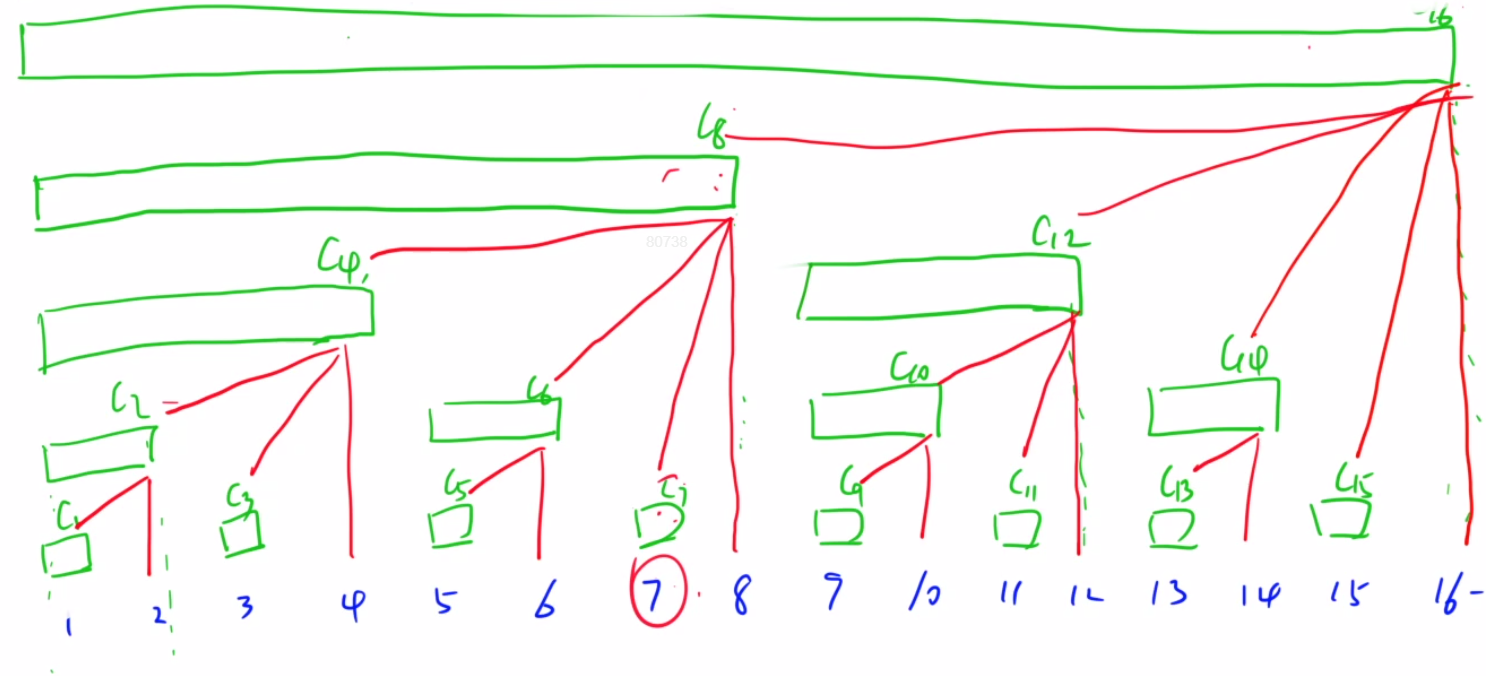
在这里面我们可以看出来，当x为奇数的时候我们c数组长度只有一个，这个很正常，因为奇数的二进制表达最低位是1，那么lowbit(odd) = 1。

c数组可以最少被哪些组成

像图片里面的红线画出来的组成关系，我们可以写成：
$$
c[16] = a[16] + c[15] + c[14] + c[12] + c[8]\
c[14] = a[14] + c[13]\
c[12] = a[12] + c[11] + c[10]\
…\
c[2] = a[2] + c[1]
$$
在这里，我们可以发现，如果我们需要求数组a中下标1-n的元素之和。我们先写出n的二进制表达，假设我们的n是16。有：

$$16 = (100000)_2$$

我们先加上最后一个数字a[16]，那么还剩下1-15下标元素之和（这个操作是为了方便用c数组表达），我们可以表达成：

$$15 = (11111)_2$$

这样的话我们可以使用lowbit操作和c数组来将这个组合起来：
$$
sum[0001,1111] = sum\bigl(1110,1111\bigr] + sum\bigl(1100,1110\bigr] + sum\bigl(1000,1100\bigr] + sum\bigl(0000,1000\bigr]\
\Downarrow\
sum[0001,1111] = sum\bigl(1111 - 1,1111\bigr] + sum\bigl(1110 - 10,1110\bigr] + sum\bigl(1100 - 100,1100\bigr] + sum\bigl(1000 - 1000,1000\bigr]\
\Downarrow\
sum[0001,1111] = sum\bigl(1111 - 1,1111\bigr] + sum\bigl(1111 - 1 - 10,1111 - 1\bigr] + sum\bigl(1111 - 1 - 10 - 100,1111 - 1 - 10\bigr] + sum\bigl(1111 - 1 - 10 - 100 - 1000,1111 - 1 - 10 - 100\bigr]\
\Downarrow\
sum[1,15] = sum\bigl(2^4 - 1 - 2^0,2^{4} - 1\bigr] + sum\bigl(2^4 - 2^0 - 1 - 2^1,2^{4} - 2^0 - 1 \bigr] + sum\bigl(2^4 - 2^0 - 1 - 2^1 - 2^2,2^{4} -2^0 - 1 - 2^1\bigr] + sum\bigl(2^4 - 2^0 - 1 - 2^1 - 2^2 - 2^3,2^4 - 2^0 - 1 - 2^1 - 2^2]\
\Downarrow\
sum[1,15] = sum\bigl(16 - 1 - lowbit(16 - 1) - 2^0,16 - 1\bigr]\ + sum\bigl(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)),16 - 1 - lowbit(16 - 1) \bigr]\ + sum\bigl(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)) - lowbit(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1))),16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1))\bigr]\ + sum\bigl(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)) - lowbit(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1))) - lowbit(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)) - lowbit(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)))),16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)) - lowbit(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)))\bigr]\
\Downarrow\
sum[1,15] = c[16-1] \+ c[16-1 - lowbit(16 - 1)]\ + c[16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1))]\+c[16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)) - lowbit(16 - 1 - lowbit(16 - 1) - lowbit(16 - 1 - lowbit(16 - 1)))]\
\Downarrow\
sum[1,15] = c[15] + c[15 - lowbit(15)] + c[14] - c[lowbit(14)] +c[12] - c[12 - lowbit(12)]\
\Downarrow\
sum[1,15] = c[15] + c[14] + c[12] + c[8]
$$
深入理解

求1-n的元素之和，我们每次都要做n-1的操作的原因其实是根据规律，每次都是要加上a[n]，这个操作对应-1。后面的-lowbit(x) 操作是对应+ c[x]操作。

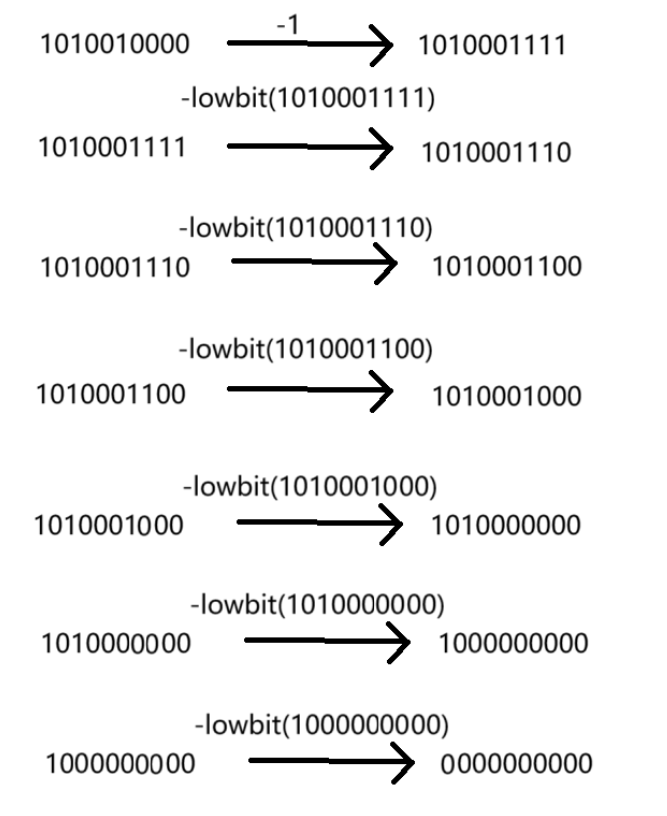
可以使用伪代码来表示我们求sum[1,n]的下标元素之和：

1
2
3

int res = a[n];
for(int i = n;i > 0;i - lowbit(i))
    res += c[i];

修改某个数字，对应需要修改哪些父节点

以下是我的胡言乱语~~

只要理解了c数组是被哪些组成之后，我们很好可以理解修改的过程，如下图所示，我们修改了第七的元素，我们第七个元素的直接父节点是c[8]，c[8]在直接父节点是c[16]。我们首先拿出结论，我们x的直接父节点是x + lowbit(x)。原因是：我们求c[parent]的直接子节点，也就是求c[parent]是最少能被哪些元素直接组成的，这个过程我们首先执行parent - 1。假设parent等于28，二进制表达式为(11100)，我们首先算出27的二进制表达式也就是(11011)。根据lowbit操作，我们所有的子节点应该是(11010)，(11000)，(10000)。因为这些是从1-28的我们的c[28]应该是(28-lowbit(28),28]，也就是(24,28]化成二进制就是(11000,11100]。所以c[28]的直接子节点就是c[11010]和a[11100]和c[11011]。但是在这里面我们的a是不算的，因为我们改了a需要改的是c只统计c。所以直接子节点就是11010和11011。其实从这么看我们直接子节点就是从(n - lowbit(n),n]中取得，n是减去1之后的结果，那么我们的子节点其实二进制里面最高位到lowbit(n)上每一位是和n+1相同的。又因为我们减去了1。所以lowbit这一位肯定是0，讲起来有点绕，可以这么理解，父节点一定是x + lowbit(x)。

使用伪代码实现找到父节点

1 2	for(int i = x;i <= n;i += lowbit(i)) c[i] += k;