NIM游戏

题目描述

给定 n 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 n。

第二行包含 n个数字，其中第 i 个数字表示第 i 堆石子的数量。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围

1≤n≤105,
1≤每堆石子数≤109

输入样例：

1
2
2
2 3

输出样例：

1
Yes

解题思路：

首先介绍一个概念就是必胜态和必败态。这都是先手状态。必胜态表示某种方式可以转化成必败态。必败态表示不管怎么操作的状态都是必胜态。

先给出这个题目的结论：

  • 所有石子的异或为0，那么就是必败态
  • 所有石子的异或非0，那么就是必胜态

需要证明，为什么异或非0可以转化成异或为0？首先，我们假设异或结果为x。x的二进制最高位为k。那么在石堆中肯定含有大于2^(k-1)的石堆。我们假设这堆式子为ai个。那么我们可以知道ai ^ x 一定小于 ai（不管k位后怎么变，k位变0了）。因为ai ^ x < ai，所以我们可以从石堆ai中拿(ai - ai ^ x)个石堆，就可以得到原来ai个石头的石堆变成了(ai - (ai - ai ^ x)) = ai ^ x。最后的异或结果就是0。

集合-NIM游戏

题目描述

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 k，表示数字集合 S 中数字的个数。

第二行包含 k 个整数，其中第 i 个整数表示数字集合 S 中的第 i 个数 si。

第三行包含整数 n。

第四行包含 n 个整数，其中第 i 个整数表示第 i 堆石子的数量 hiℎ。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围

1≤n,k≤100
1≤si,hi≤10000

输入样例：

1
2
3
4
2
2 5
3
2 4 7

输出样例：

1
Yes

题目思想

先讲一下两个概念：

  1. mex运算：mex{a1,a2,a3,a4}也就是找到集合里面到达不了的最小非负数，例如mex{1,2,3,5} = 0。
  2. sg函数：在博弈论中，每个状态都可以转化成别的状态，最后成为下面的图，我们定义没有出边的为必败态，sg(没有出边的点) = 0。每个点的sg值等于他指向所有节点sg值得mex运算。
  3. 我们可以看见如果sg值 = 0。那么说明他的子节点走不到0。那就是必败态。如果sg ！= 0，就说明这个点可以走到0。是必胜态。

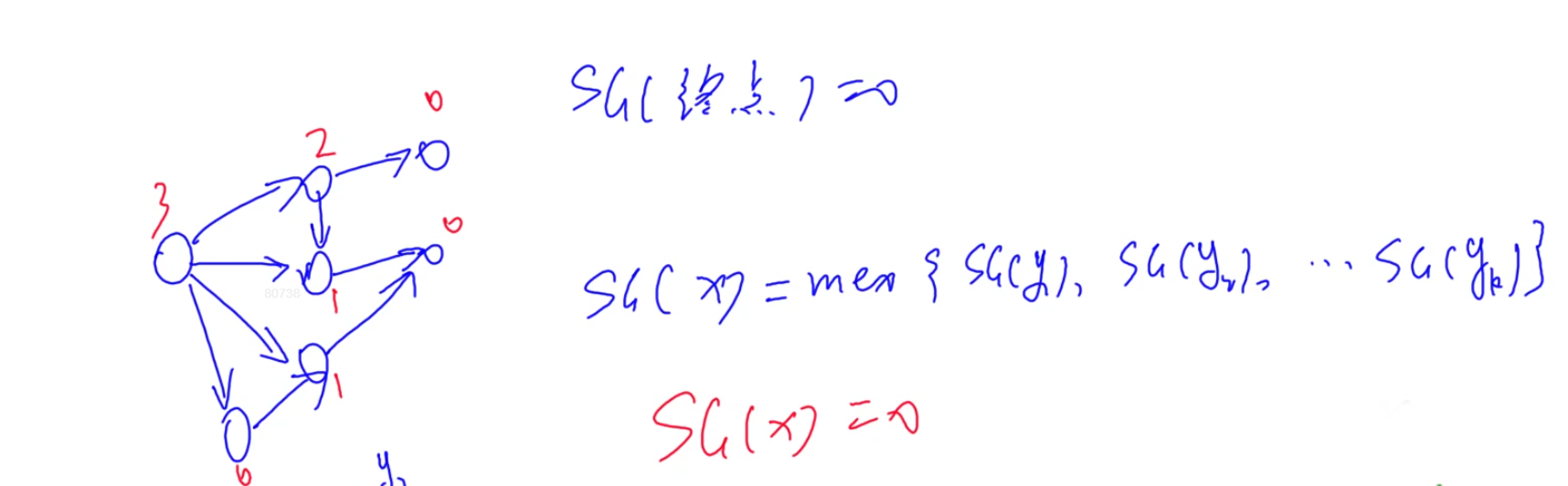
但是为什么我们不是0和1的取值呢？因为在很多题目中这个图不止一个，可能有很多，我们操作不一定在一张图上操作，这种情况下我们sg值就会起作用了。

为什么我们全部异或是0就是必败呢？我们可以类比第一个NIM游戏。如果x ！= 0 。我们可以随机拿走ai - (ai ^ x)个石头转化成必败态。但是在我们这里，相当于我们将ai状态转换成x状态。因为mex操作是到不了的最小值。如果ai ！= 0。那么这个状态可以走到0-ai-1所有状态。

题目代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Main{
    public static int N = 110,M = 10010,k;
    public static int[] sg = new int[M],num = new int[N];
    
    public static Scanner sc = new Scanner(System.in);
    
    //加了记忆化搜索
    public static int sg(int x){
        if(sg[x] != -1) return sg[x];
        Set<Integer> set = new HashSet<>();
        for(int i = 1;i <= k;i++)
            if(x >= num[i])
                set.add(sg(x - num[i]));
        
        for(int i = 0;;i++)
            if(!set.contains(i))
                return (sg[x] = i);
    }
    
    public static void main(String[] args){
        k = sc.nextInt();
        for(int i = 1;i <= k;i++) num[i] = sc.nextInt();
        Arrays.fill(sg,-1);
        int res = 0,n = sc.nextInt();
        for(int i = 1;i <= n;i++)
            res ^= sg(sc.nextInt());
            
        if(res == 0) System.out.println("No");
        else System.out.println("Yes");
        
    }
}

注意：如果一个必胜态或者必败态分的状态里面是一个sg集合，那么这个状态的sg就是sg集合的异或值。