题目描述
给出一个有向无环的连通图,起点为 1,终点为 N,每条边都有一个长度。
数据保证从起点出发能够到达图中所有的点,图中所有的点也都能够到达终点。
绿豆蛙从起点出发,走向终点。
到达每一个顶点时,如果有 K 条离开该点的道路,绿豆蛙可以选择任意一条道路离开该点,并且走向每条路的概率为 1/K。
现在绿豆蛙想知道,从起点走到终点所经过的路径总长度的期望是多少?
输入格式
第一行: 两个整数 N,M代表图中有 N 个点、M 条边。
第二行到第 1+M 行: 每行 33 个整数 a,b,c代表从 a到 b有一条长度为 c 的有向边。
输出格式
输出从起点到终点路径总长度的期望值,结果四舍五入保留两位小数。
数据范围
1≤N≤105,
1≤M≤2N
输入样例:
1
2
3
4
5
| 4 4
1 2 1
1 3 2
2 3 3
3 4 4
|
输出样例:
解题思路
如下图有向无环图,其中黑色为点的编号,红色为路径长度。
我们可以知道1->3->5->7 的一条路径对期望的贡献是 $\frac{1}{3} \times \frac{1}{2} \times 1 \times (2 + 3 + 1)$。
1->3->6->7的一条路径对期望的贡献是 $\frac{1}{3} \times \frac{1}{2} \times 1 \times (2 + 1 + 5)$。
这就是从起点经过3的对期望的贡献,加起来可以是$\frac{1}{3} \times (2 + 1 \times (3 + 1) + 1 \times (1 + 5))$。
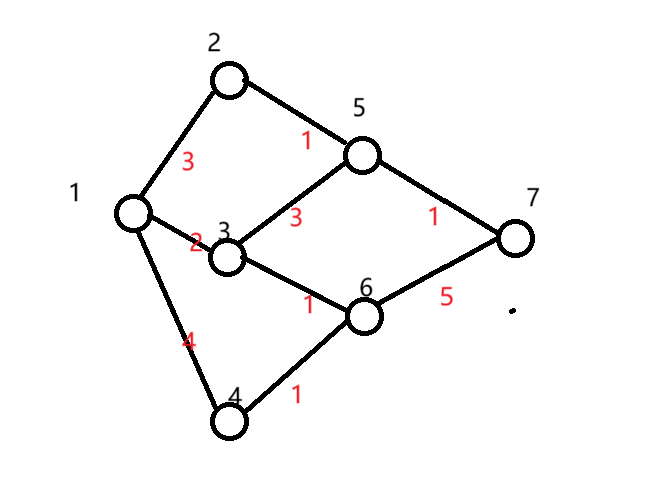
接下来我们其实就可以开始计算总期望了,我们可以使用期望dp来实现。其中dp[i]代表从i出发,到终点的期望。我们可以遍历这个图,计算期望,需要从重点往起点计算。
解题代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Main{
public static int N = 100010,M = 2*N,idx;
public static double res;
public static int[] ne = new int[M],e = new int[M],h = new int[N],out = new int[N],w = new int[M];
public static double[] f = new double[N];
public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static void insert(int a,int b,int w1){
e[idx] = b;
w[idx] = w1;
ne[idx] = h[a];
h[a] = idx++;
}
public static double dp(int x){
if(f[x] >= 0) return f[x];
f[x] = 0;
for(int i = h[x];i != -1;i = ne[i]){
f[x] += (w[i] + dp(e[i]) )/ out[x];
}
return f[x];
}
public static void main(String[] args)throws Exception{
String[] s1 = br.readLine().split(" ");
int n = Integer.parseInt(s1[0]),m = Integer.parseInt(s1[1]);
Arrays.fill(h,-1);
Arrays.fill(f,-1);
for(int i = 1;i <= m;i++){
String[] s2 = br.readLine().split(" ");
int a = Integer.parseInt(s2[0]),b = Integer.parseInt(s2[1]),w = Integer.parseInt(s2[2]);
insert(a,b,w);
out[a] ++;
}
double res = dp(1);
System.out.printf("%.2f",res);
}
}
|

