题目描述
Admin 生日那天,Rainbow 来找 Admin 玩扑克牌。
玩着玩着 Rainbow 觉得太没意思了,于是决定给 Admin 一个考验。
Rainbow 把一副扑克牌(5454 张)随机洗开,倒扣着放成一摞。
然后 Admin 从上往下依次翻开每张牌,每翻开一张黑桃、红桃、梅花或者方块,就把它放到对应花色的堆里去。
Rainbow 想问问 Admin,得到 A张黑桃、B 张红桃、C 张梅花、D 张方块需要翻开的牌的张数的期望值 E 是多少?
特殊地,如果翻开的牌是大王或者小王,Admin 将会把它作为某种花色的牌放入对应堆中,使得放入之后 E的值尽可能小。
由于 Admin 和 Rainbow 还在玩扑克,所以这个程序就交给你来写了。
输入格式
输入仅由一行,包含四个用空格隔开的整数,A,B,C,D。
输出格式
输出需要翻开的牌数的期望值 E,四舍五入保留 33 位小数。
如果不可能达到输入的状态,输出 -1.000。
数据范围
0≤A,B,C,D≤15
输入样例:
输出样例:
解题思路
我们可以把这个题目,翻每一张牌的过程,抽象到一个状态到另一个状态上,也就是我们最后翻牌的过程可以抽象成一个图的形状。我们只需要计算起点到终点的期望就好了。其中我们使用状态f[a][b][c][d][x][y]表示当前状态,当前得到了得到 a 张黑桃、b 张红桃、c 张梅花、d 张方块,x = 0 的时候表示大王还没有翻出来,x = 1,2,3,4分别表示我们的大王放到了黑桃,红桃,梅花和方块中。y类似x。我们的起点是f[0][0][0][0][0][0],终点有很多,只要满足(a + (x == 1) + (y == 1)) == A && (b + (x == 2) + (y == 2)) == B ......就可以了。我们每个点可以向六个方向转化。
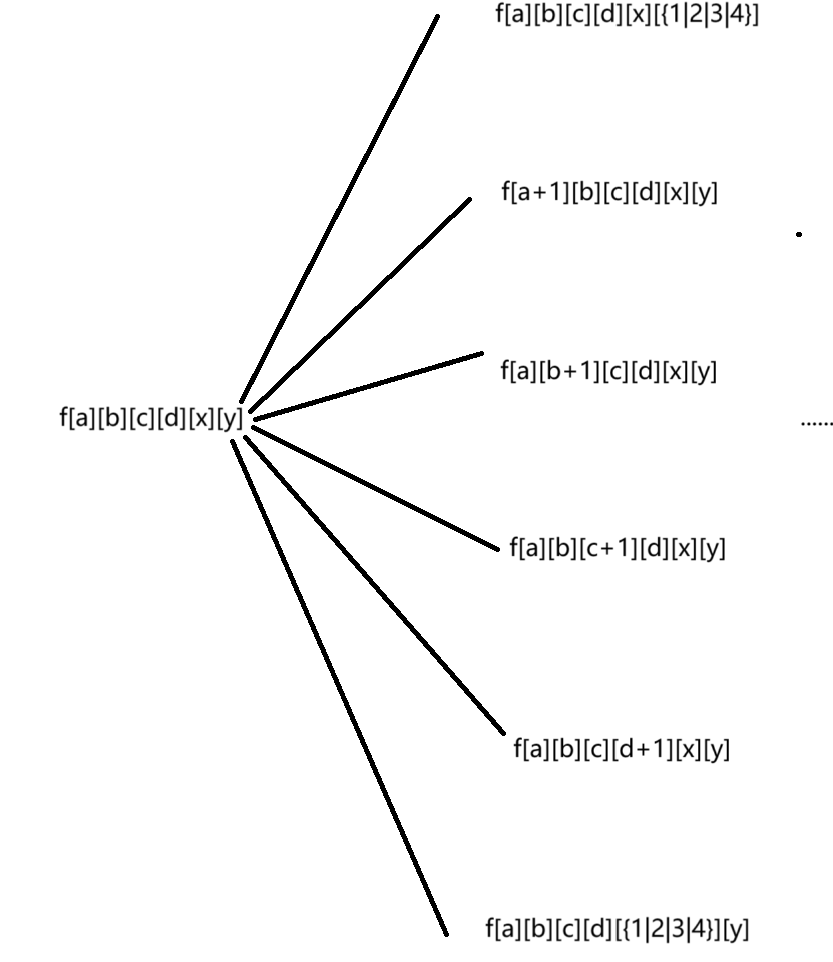
其中我们可以计算每个路径的对应概率:
sum = a + b + c + d + (x != 0) + (y != 0)
注意
- 在这里面我们输出的是需要翻开的牌数的期望值 E,所以我们每一张牌的值都是1。
- 走不到的情况其实就是超出了已有的牌数,就肯定走不到。
- 我们求的翻开牌数的期望值,肯定包括翻完了到不了终点的方法,所以我们所有情况都要搜索。
解题代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| class Main{
public static int N = 20,A,B,C,D;
public static double[][][][][][] dp = new double[N][N][N][N][5][5];
public static Scanner sc = new Scanner(System.in);
public static double dfs(int a,int b,int c,int d,int x,int y){
if(dp[a][b][c][d][x][y] >= 1e-7) return dp[a][b][c][d][x][y];
int a_s = a + (x == 1 ? 1 : 0) + (y == 1 ? 1 : 0);
int b_s = b + (x == 2 ? 1 : 0) + (y == 2 ? 1 : 0);
int c_s = c + (x == 3 ? 1 : 0) + (y == 3 ? 1 : 0);
int d_s = d + (x == 4 ? 1 : 0) + (y == 4 ? 1 : 0);
int sum = a + b + c + d + (x != 0 ? 1 : 0) + (y != 0 ? 1 : 0);
if(a_s >= A && b_s >= B && c_s >= C && d_s >= D) return (dp[a][b][c][d][x][y] = 0);
double res = 1;
if(a < 13) res += ((double)13 - a) / (54 - sum) * dfs(a+1,b,c,d,x,y);
if(b < 13) res += ((double)13 - b) / (54 - sum) * dfs(a,b+1,c,d,x,y);
if(c < 13) res += ((double)13 - c) / (54 - sum) * dfs(a,b,c+1,d,x,y);
if(d < 13) res += ((double)13 - d) / (54 - sum) * dfs(a,b,c,d+1,x,y);
if(x == 0){
double min = 0x3f3f3f3f;
for(int i = 1;i <= 4;i++){
min = Math.min(min,dfs(a,b,c,d,i,y));
}
res += (double)1 / (54 - sum) * min;
}
if(y == 0){
double min = 0x3f3f3f3f;
for(int i = 1;i <= 4;i++){
min = Math.min(min,dfs(a,b,c,d,x,i));
}
res += (double)1 / (54 - sum) * min;
}
return (dp[a][b][c][d][x][y] = res);
}
public static void main(String[] args){
A = sc.nextInt();B =sc.nextInt();C = sc.nextInt();D = sc.nextInt();
if(Math.max(0,A - 13) + Math.max(B-13,0) + Math.max(C-13,0) + Math.max(D-13,0) > 2){
System.out.print("-1.000");
return;
}
System.out.printf("%.3f",dfs(0,0,0,0,0,0));
}
}
|

