题目描述
众所周知,“八皇后” 问题是求解在国际象棋棋盘上摆放 88 个皇后,使得两两之间互不攻击的方案数。
已经学习了很多算法的小蓝觉得 “八皇后” 问题太简单了,意犹未尽。作为一个国际象棋迷,他想研究在 N×M的棋盘上,摆放 K 个马,使得两两之间互不攻击有多少种摆放方案。
由于方案数可能很大,只需计算答案除以 1000000007 (即 109+7) 的余数。
如下图所示,国际象棋中的马摆放在棋盘的方格内,走 “日” 字,位于 (x,y) 格的马(第 x 行第 y 列)可以攻击 (x+1,y+2)、(x+1,y−2)、(x−1,y+2)、(x−1,y−2)、(x+2,y+1)、(x+2,y−1)(+2,−1)、(x−2,y+1)(−2,+1) 和 (x−2,y−1) 共 88 个格子。
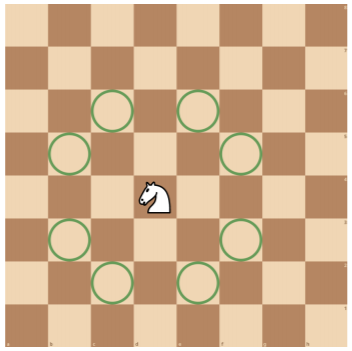
输入格式
输入一行包含三个正整数 N,M,K分别表示棋盘的行数、列数和马的个数。
输出格式
输出一个整数,表示摆放的方案数除以 1000000007 (即 109+7) 的余数。
数据范围
对于 5%的评测用例,K=1;
对于另外 10%的评测用例,K=2;
对于另外 10%的评测用例,N=1;
对于另外 20% 的评测用例,N,M≤6,K≤5;
对于另外 25%的评测用例,N≤3,M≤20,K≤12;
对于所有评测用例,1≤N≤6,1≤M≤100,1≤K≤20。
输入样例1:
输出样例1:
输入样例2:
输出样例2:
输入样例3:
输出样例3:
解题思路
dfs
这个题目暴力做法可以过一半的用例,主要就是为了遍历每个马在不在当前位置放置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| import java.io.*;
import java.util.*;
class Main{
public static int N = 10,M = 110,K = 30,res = 0,n,m,k;
public static int[][] g = new int[N][M];
public static int[] checkx = {2,-2,1,-1,2,-2,1,-1},checky = {1,1,2,2,-1,-1,-2,-2};
public static Scanner sc = new Scanner(System.in);
public static void dfs(int x,int y,int d){
if(d == k){
res = (int)((long)res + 1) % 1000000007;
return;
}
if(x > n || y > m) return;
int index = 0;
for(int l = 0;l < 8;l++){
int fx = x + checkx[l],fy = y + checky[l];
if(fx < 1 || fy < 1 || fx > n || fy > m ) continue;
if(g[fx][fy] == 1){
index = 1;
break;
}
}
int tx = x + (y + 1) / (m + 1);
int ty = (y + 1 == m + 1 ? 1 : y + 1);
if(index == 0){
g[x][y] = 1;
dfs(tx,ty,d+1);
g[x][y] = 0;
}
dfs(tx,ty,d);
}
public static void main(String[] args){
n = sc.nextInt();m = sc.nextInt();k = sc.nextInt();
dfs(1,1,0);
System.out.println(res);
}
}
|
状态压缩dp
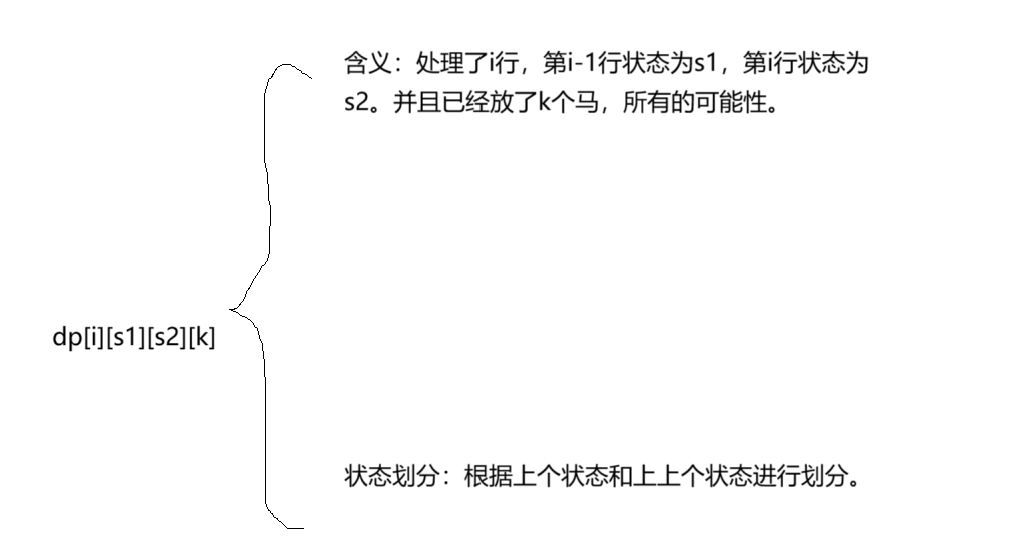
注意:如果使用滚动数组,记住,需要清零。并且我们需要注意两个二进制数的判断。如果想判断i第1位是不是1.是 (i & (1 << 1)) != 0不是 (i & (1 << 1)) == 1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| import java.io.*;
import java.util.*;
class Main{
public static int N = 6,M = 110,K = 30,P = 1000000007;
public static int[] index = new int[N];
public static int[][] g = new int[M][M];
public static int[][][][] dp = new int[M][1 << N][1<<N][K];
public static Scanner sc = new Scanner(System.in);
public static int lowbit(int x){
return (-x) & x;
}
public static int get(int x){
int res = 0;
while(x > 0){
x -= lowbit(x);
res++;
}
return res;
}
public static void main(String[] args){
int n = sc.nextInt(),m = sc.nextInt(),kk = sc.nextInt();
dp[0][0][0][0] = 1;
for(int i = 1;i <= m + 2;i++){
for(int s1 = 0;s1 < (1 << n);s1++){
for(int s2 = 0;s2 < (1 << n);s2++){
if(((s1>>2) & s2) != 0 || (s1 & (s2 >> 2)) != 0) continue;
for(int j = 0;j < (1 << n);j++){
if((s1 & (j >> 1)) != 0 || ((s1 >> 1) & j ) != 0 ) continue;
if(((s2 >> 2) & j ) != 0 || (s2 & (j >> 2)) != 0 ) continue;
for(int k = get(j);k <= kk;k++){
dp[i][s2][j][k] = (int)(((long)dp[i][s2][j][k] + dp[i-1][s1][s2][k - get(j)]) % P);
}
}
}
}
}
System.out.println(dp[m+2][0][0][kk]);
}
}
|


