题目
直方图是由在公共基线处对齐的一系列矩形组成的多边形。
矩形具有相等的宽度,但可以具有不同的高度。
例如,图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图,矩形的宽度都为1:
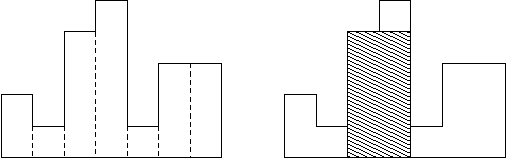
通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数n开始,表示组成直方图的矩形数目。
然后跟随n个整数$h_1,…,h_n$。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为1。
同行数字用空格隔开。
当输入用例为n=0时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。
数据范围
$1≤n≤100000,0≤h_i≤1000000000$
输入样例
1
2
3
| 7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
|
输出样例
解题思路
暴力思路
这个题目求得就是连续的矩阵能够组成一个最大的矩阵,要求最后的矩阵高度是所有矩阵中最小的那一个。从高度入手,我们如果确定了高度,我们就可以确定这个矩阵是由哪些矩阵组成。这个高度其实就是每一个矩阵的高度其中之一。所以暴力解法就是枚举每一个矩阵,从每个矩阵开始向外延伸,直到遇见了比我们矩阵高度矮的就停止。就可以确定左边界和右边界。这样的做法是O(n^2)
单调栈思路
我们可以使用单调栈来确认每个矩阵中左边或者右边第一个比他小的数字的下标,这样我们就可以用O(n)的时间来确认出以每个矩阵高度确认的最终矩阵的大小。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| import java.io.*;
import java.util.*;
class Main{
public static int N = 100010;
public static int[] a = new int[N],l = new int[N],r = new int[N];
public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args)throws Exception{
String[] s1 = br.readLine().split(" ");
while(Integer.parseInt(s1[0]) != 0){
int n = Integer.parseInt(s1[0]);
for(int i = 1;i <= n;i++) a[i] = Integer.parseInt(s1[i]);
int[] stack = new int[N];
int hh = 0;
for(int i = 1;i <= n;i++){
while(hh != 0 && a[i] <= a[stack[hh]]) hh--;
l[i] = stack[hh] + 1;
stack[++hh] = i;
}
Arrays.fill(stack,0);
hh = 0;
stack[0] = n+1;
for(int i = n;i >= 1;i--){
while(hh != 0 && a[i] <= a[stack[hh]]) hh--;
r[i] = stack[hh] - 1;
stack[++hh] = i;
}
long res = 0;
for(int i = 1;i <= n;i++){
res = Math.max(res,((long)r[i] - l[i] + 1) * a[i]);
}
bw.write(res+"\n");
s1 = br.readLine().split(" ");
}
bw.flush();
}
}
|

