逆序对问题汇总

一直以来，求序列中的逆序对都是比较基础的问题，但是这个问题的延伸困扰了作者很久。简单的逆序队就是可以用归并排序和树状数组来求。但是逆序对可以扩展对无序序列排序，相邻的数字交换最小值其实就是逆序对的数量。下面我们来对这些问题进行一个总结。

定义

顾名思义，逆序对其实就是在序列$a_i$中，当$i < j$并且$a_i > a_j$时，我们将$a_i$和$a_j$统称为逆序对。当然逆序对的求法也可以总结成两种，一种是归并排序，记录每次交换的时候逆序对的数量。一种是树状数组，记录每个元素前面比他大的值并且后面比他小的值。

这里可以参考原始的求逆序对的数量

还有一种题目就是求序列无序到有序，需要交换多少次相邻数字，其实这个也是逆序对数量。这个思想其实就是冒泡排序的思想，可以参考下面的图片，我们每个数字最少需要交换多少次，可以这个数字参考前面和后面有多少个逆序对。

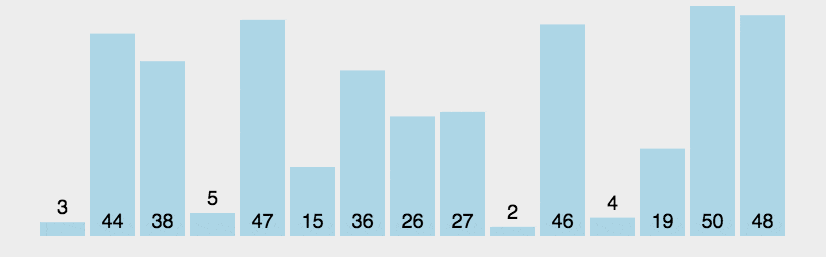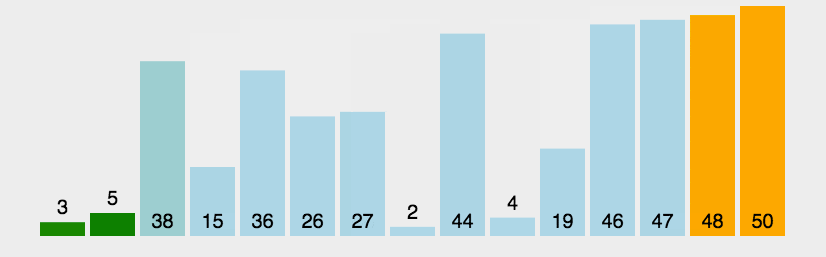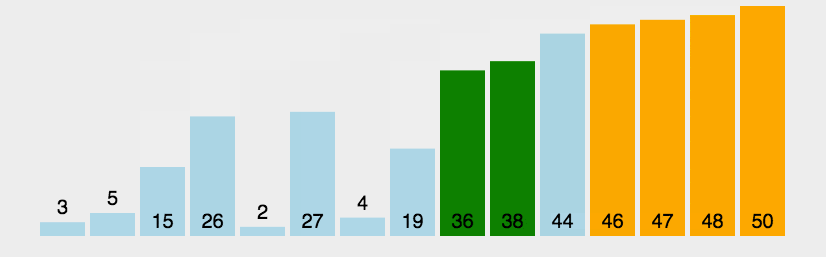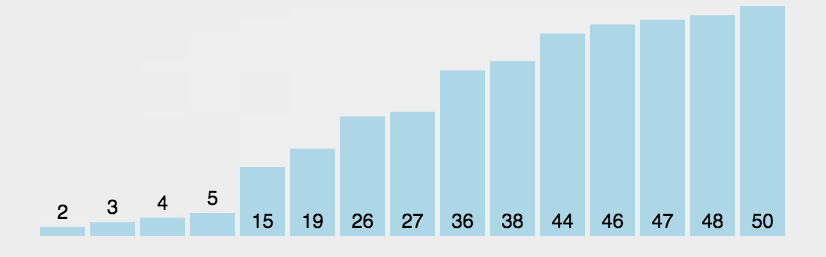
可以参考这个题目小朋友排队。还需要注意，如果我们使用树状数组求逆序对，需要进行一个离散化。