[NOIP2013 提高组] 火柴排队

题目背景

NOIP2013 提高组 D1T2

题目描述

涵涵有两盒火柴，每盒装有 $n$ 根火柴，每根火柴都有一个高度。 现在将每盒中的火柴各自排成一列， 同一列火柴的高度互不相同， 两列火柴之间的距离定义为：$ \sum (a_i-b_i)^2$。

其中 $a_i$ 表示第一列火柴中第 $i$ 个火柴的高度，$b_i$ 表示第二列火柴中第 $i$ 个火柴的高度。

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 $10^8-3$ 取模的结果。

输入格式

共三行，第一行包含一个整数 $n$，表示每盒中火柴的数目。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。

第三行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

输出格式

一个整数，表示最少交换次数对 $10^8-3$ 取模的结果。

样例 #1

样例输入 #1

1
2
3
4
2 3 1 4
3 2 1 4

样例输出 #1

1
1

样例 #2

样例输入 #2

1
2
3
4
1 3 4 2
1 7 2 4

样例输出 #2

1
2

提示

输入输出样例说明一

最小距离是 $ 0$，最少需要交换 $1$ 次，比如：交换第 $1 $ 列的前 $ 2$ 根火柴或者交换第 $2$ 列的前 $2 $ 根火柴。

输入输出样例说明二

最小距离是 $10$，最少需要交换 $2$ 次，比如：交换第 $1$ 列的中间 $2$ 根火柴的位置，再交换第 $2$ 列中后 $2$ 根火柴的位置。

数据范围

对于 $10%$ 的数据， $1 \leq n \leq 10$；

对于 $30%$ 的数据，$1 \leq n \leq 100$；

对于 $60%$ 的数据，$1 \leq n \leq 10^3$；

对于 $100%$ 的数据，$1 \leq n \leq 10^5$，$0 \leq$ 火柴高度 $< 2^{31}$。

解题思路

​ 首先我们可以用贪心证明，当我们两个序列都是有序排列一一对应的时候$\sum_{i}(a_i - b_i)^2$可以取最小值，以下是反证法：我们原有序列有序 也就是$a_1 < a_2$并且$b_1 < b_2$。那么我们的和就是$(a_1 - b_1)^2 + (a_2 - b_2)^2$。假设我们的序列无序，其实对应我们将$a_1$和$a_2$对调得到这个假设情况下的和就是$(a_2 - b_1)^2 + (a_1 - b_2)^2$。前者减去后者我们会得到$2(a_2-a_1)(b_1-b_2) $这个结果肯定是小于0的。那么就是说我们的有序情况下肯定是最小的，假设不成立。

​ 我们可以继续分析，其实不一定需要两个序列都有序才会使交换次数最小，我们只要两者位置对应和有序的时候位置对应一样就好了。在这里我们先简化问题，如果a序列有序，b序列无序，那么我们最小的交换次数其实就是把b序列变成有序的交换次数。

​

​ 但是如果我们当a，b序列都无序的情况下，我们可以想办法让a变成有序，然后再计算b的逆序数就好了，这个情况下我们用到映射。我们将a序列按照他的位置进行映射，最后形成一个映射表。最后根据映射表映射b序列，这样我们最后改变b序列就好了。

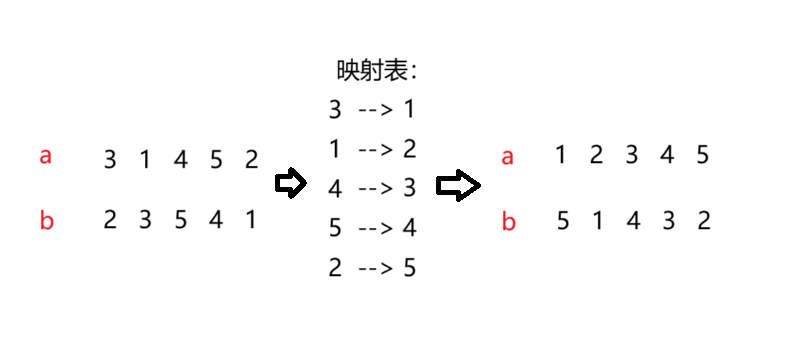
​ 这样我们就可以解决问题，但是在这里我们需要进行一个离散化才可以。这里的离散化方法可以参考这个方法。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import java.io.*;
import java.util.*;

class Main{
    public static int N = 100010,n,P = 99999997;
    public static long res;
    public static Integer[] a = new Integer[N],b = new Integer[N],p = new Integer[N],temp = new Integer[N],c = new Integer[N];
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    
    //离散化a
    public static void work(Integer[] a){
        for(int i = 1;i <= n;i++) p[i] = i;
        Arrays.sort(p,1,n+1,new Comparator<Integer>(){
            public int compare(Integer o1,Integer o2){
                return a[o1] - a[o2];
            }
        });
        for(int i = 1;i <= n;i++) a[p[i]] = i;
    }
    
    public static void sort(Integer[] a,int l,int r){
        if(l >= r) return;
        int mid = (l + r) >> 1;
        sort(a,l,mid);
        sort(a,mid+1,r);
        int i = l,j = mid+1,k = i;
        while(i <= mid && j <= r){
            if(a[i] <= a[j])
                temp[k++] = a[i++];
            else{
                temp[k++] = a[j++];
                res = (res +  (mid - i + 1)) % P;
            }
        }
        while(i <= mid)
            temp[k++] = a[i++];
        while(j <= r)temp[k++] = a[j++];
        for(i = l;i <= r;i++) a[i] = temp[i];
    }
    
    public static void main(String[] args)throws Exception{
        n = Integer.parseInt(br.readLine());
        
        String[] s1 = br.readLine().split(" ");
        for(int i = 1;i <= n;i ++) a[i] = Integer.parseInt(s1[i-1]);
        String[] s2 = br.readLine().split(" ");
        for(int i = 1;i <= n;i ++) b[i] = Integer.parseInt(s2[i-1]);
        work(a);
        work(b);
        //记录一下映射表
        for(int i = 1;i <= n;i ++) c[a[i]] = i;
        for(int i = 1;i <= n;i ++) b[i] = c[b[i]];
        sort(b,1,n);
        System.out.println(res);
    }
}