[IOI2000] 回文字串

题目背景

IOI2000 第一题

题目描述

回文词是一种对称的字符串。任意给定一个字符串，通过插入若干字符，都可以变成回文词。此题的任务是，求出将给定字符串变成回文词所需要插入的最少字符数。

比如 $\verb!Ab3bd!$ 插入 $2$ 个字符后可以变成回文词 $\verb!dAb3bAd!$ 或 $\verb!Adb3bdA!$，但是插入少于 $2$ 个的字符无法变成回文词。

注意：此问题区分大小写。

输入格式

输入共一行，一个字符串。

输出格式

有且只有一个整数，即最少插入字符数。

样例 #1

样例输入 #1

1
Ab3bd

样例输出 #1

1
2

提示

数据范围及约定

记字符串长度为 $l$。

对于全部数据，$0<l\le 1000$。

思路

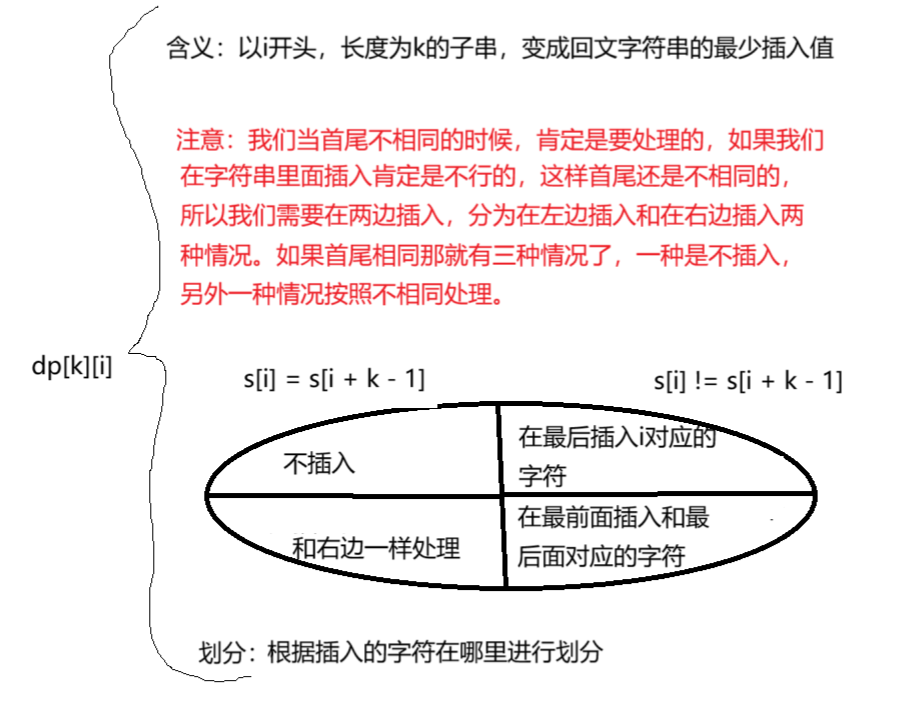
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Main {
    public static int N = 1010;
    public static int[][] dp = new int[N][N];
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws  Exception{
        String s = br.readLine();
        int n = s.length();
        for(int i = 1;i <= n;i++){
            Arrays.fill(dp[i],0x3f3f3f3f);
            dp[1][i] = dp[0][i] = 0;
        }

        for(int len = 2;len <= n;len++){
            for(int i = 1;i + len - 1 <= n;i++){
                int j = i + len - 1;
                if(s.charAt(i-1) == s.charAt(j-1))
                    dp[len][i] = Math.min(dp[len-2][i+1],Math.min(dp[len - 1][i + 1] + 1,dp[len - 1][i] + 1));
                else dp[len][i] = Math.min(dp[len-1][i] + 1,dp[len-1][i+1] + 1);
            }

        System.out.println(dp[n][1]);
    }
}