[USACO03FALL] Cow Exhibition G
题目背景
题目描述
奶牛想证明它们是聪明而风趣的。为此,贝西筹备了一个奶牛博览会,她已经对 $N$ 头奶牛进行了面试,确定了每头奶牛的智商和情商。
贝西有权选择让哪些奶牛参加展览。由于负的智商或情商会造成负面效果,所以贝西不希望出展奶牛的智商之和小于零,或情商之和小于零。满足这两个条件下,她希望出展奶牛的智商与情商之和越大越好,请帮助贝西求出这个最大值。
输入格式
第一行:单个整数 $N$,$1 \le N \le 400$。
第二行到第 $N+1$ 行:第 $i+1$ 行有两个整数:$S_i$ 和 $F_i$,表示第 $i$ 头奶牛的智商和情商,− $1000 \le S_i;F_i \le 1000$。
输出格式
输出单个整数:表示情商与智商和的最大值。贝西可以不让任何奶牛参加展览,如果这样做是最好的,输出 $0$。
样例 #1
样例输入 #1
1
2
3
4
5
6
| 5
-5 7
8 -6
6 -3
2 1
-8 -5
|
样例输出 #1
提示
选择第一头,第三头,第四头奶牛,智商和为−5+6+2 = 3,情商和为7−3+1 = 5。再加
入第二号奶牛可使总和提升到10,不过由于情商和变成负的了,所以是不允许的
解题思路
这个题目首先想到01背包,我们可以吧体积固定成情商或者智商,通过固定的情商来求智商最大值,然后再遍历一遍求解。
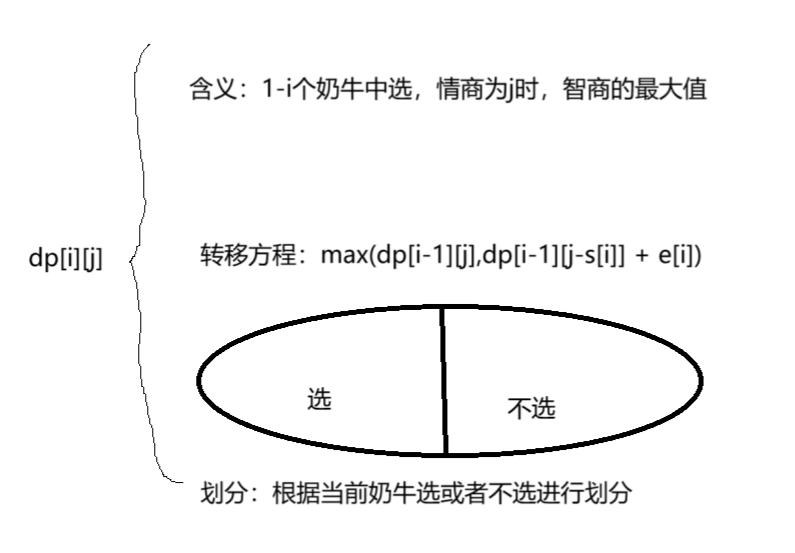
但是有一个问题就是我们的情商可能是负数,那么我们可以吧整体的j往右移动,记住这个时候我们的0点也要移动。这个时候我们就可以正常求解了。但是二维会MLE我们可以使用滚动数组优化。
代码
优化前
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| package com.zgy;
import java.util.*;
import java.io.*;
class Main {
public static int N = 410, M = N * 1010 * 2;
public static int[][] dp = new int[N][M];
public static int[] s = new int[N],f = new int[N];
public static Scanner sc = new Scanner(System.in);
public static void main(String[] args) {
int n = sc.nextInt();
for(int i = 1;i <= n;i++){
s[i] = sc.nextInt();
f[i] = sc.nextInt();
}
for(int i = 0;i <= n;i++) Arrays.fill(dp[i],-0x3f3f3f3f);
dp[0][M/2] = 0;
for(int i = 1;i <= n;i++)
for(int j = 1;j < M;j++){
dp[i][j] = dp[i-1][j];
if(j - s[i] >= 0 && j - s[i] < M && dp[i-1][j - s[i]] != -0x3f3f3f3f)
dp[i][j] = Math.max(dp[i][j],dp[i-1][j - s[i]] + f[i]);
}
int res = -0x3f3f3f3f;
for(int j = 0;j < M;j++)
if(dp[n][j] >= 0){
res = Math.max(res,dp[n][j] + j);
}
System.out.println(res - (M / 2));
}
}
|
优化后
优化成一维数组还存在一个问题,因为一维数组全是正数的时候我们的j需要倒序枚举,保证j - s[i]是没有更新过的,但是是负数的情况下就需要正序枚举。最后枚举答案需要从M/2枚举这样才能保证我们的情商都是大于等于0的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| package com.zgy;
import java.util.*;
import java.io.*;
class Main {
public static int N = 410, M = N * 1010 * 2;
public static int[] dp = new int[M];
public static int[] s = new int[N],f = new int[N];
public static Scanner sc = new Scanner(System.in);
public static void main(String[] args) {
int n = sc.nextInt();
for(int i = 1;i <= n;i++){
s[i] = sc.nextInt();
f[i] = sc.nextInt();
}
Arrays.fill(dp,-0x3f3f3f3f);
dp[M/2] = 0;
for(int i = 1;i <= n;i++)
if(s[i] < 0)
{
for(int j = 1;j < M;j++){
if(j - s[i] >= 1 && j - s[i] < M && dp[j - s[i]] != -0x3f3f3f3f)
dp[j] = Math.max(dp[j],dp[j - s[i]] + f[i]);
}
}
else{
for(int j = M - 1;j >= 1;j--){
if(j - s[i] >= 1 && j - s[i] < M && dp[j - s[i]] != -0x3f3f3f3f)
dp[j] = Math.max(dp[j],dp[j - s[i]] + f[i]);
}
}
int res = -0x3f3f3f3f;
for(int j = M/2;j < M;j++)
if(dp[j] >= 0){
res = Math.max(res,dp[j] + j);
}
System.out.println(res - (M / 2));
}
}
|

