题目

解题思路
这个题目是一个分配问题,求解每个车运送满足条件的最大的利润。我们使用贪心算法解决。
贪心和二分很像,二分是在一个线段上找到满足条件的一边,而贪心是把一个集合分为两个集合,选择一边,这一边满足最优解好于或者等于另外一边。
我们将货物按照利润从大到小进行排序,将车子按照载重从小到大进行排序,枚举车子,找到能够满足车子载重的最大利润的一个货物,这样下去就可以找到答案。
证明
我们只需要将集合分成当前的车子选择最大的利润和没有选择最大的利润两个集合:
为了证明我们的算法是有效的,我们需要证明选择最大的最优解一定好于或者等于没有选择最大的所有解法。存在两种情况:
- 所有的货车枚举完了,最大的没有被选。
这个情况我们将当前货车选择最大的,这个时候我们获得更大的利润,左边集合大于右边
- 所有的货车枚举完了,后面的选择了最大的。
如下图所示,我们当前货车选择的不是最大的,后面的火车选择了当前货车能选择的最大的货物。
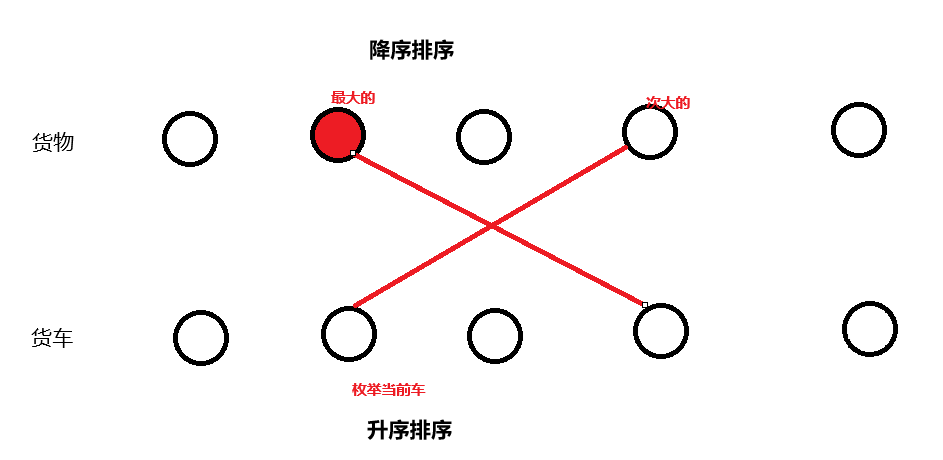
我们只需要证明交换两个车的货物,这个情况比上面的绝对不差就好。由于后面的货车载重大于前面的货车,所以我们前面也就是当前枚举的货车能载次大的货物,那么后面的也可以。我们交换之后不影响最终结果,所以得证。
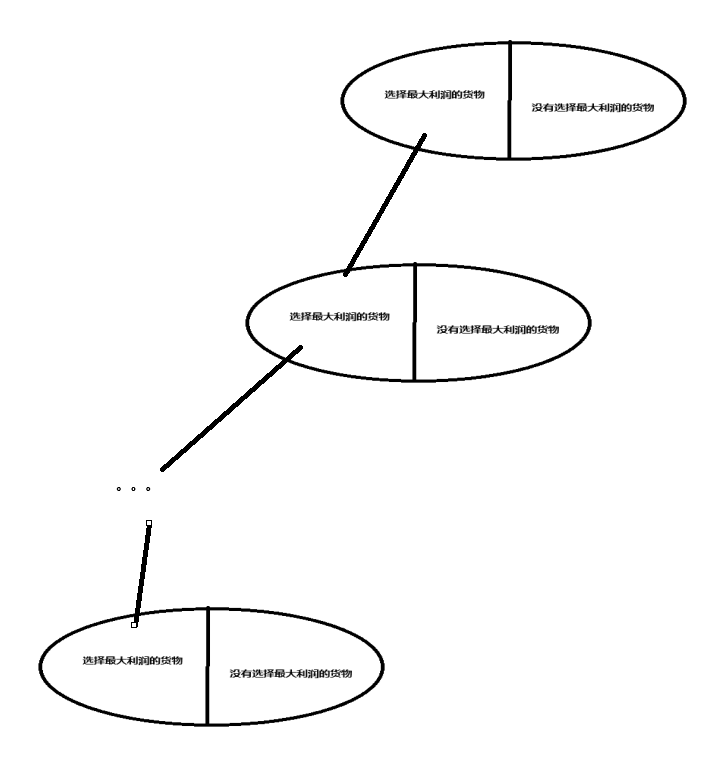
得证我们选择最大的,比不选最大的方案要好。
只要保证每次当前局部最优,最后我们选择的方案就是全局最优。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| import java.io.*;
import java.util.*;
class Main{
public static int N = 1010;
public static int[] r = new int[N],p = new int[N],stu = new int[N],record = new int[N];
public static Pair[] ps = new Pair[N];
public static Car[] car = new Car[N];
public static Scanner sc = new Scanner(System.in);
public static void main(String[] args){
int n = sc.nextInt();
for(int i = 1;i <= n;i ++) ps[i] = new Pair(i,sc.nextInt(),sc.nextInt());
Arrays.sort(ps,1,n+1,new Comparator<Pair>(){
public int compare(Pair o1,Pair o2){
return o2.p - o1.p;
}
});
int k = sc.nextInt();
for(int i = 1;i <= k;i ++) car[i] = new Car(i,sc.nextInt());
Arrays.sort(car,1,k+1,new Comparator<Car>(){
public int compare(Car o1,Car o2){
return o1.r - o2.r;
}
});
int resindex = 0,res = 0;
for(int i = 1;i <= k;i++){
for(int j = 1;j <= n;j++){
if(stu[ps[j].index] == 0&& car[i].r >= ps[j].c){
stu[ps[j].index] = 1;
res += ps[j].p;
resindex++;
record[ps[j].index] = car[i].index;
break;
}
}
}
System.out.println(resindex+" "+res);
for(int i = 1;i <= n;i++){
if(record[i] == 0) continue;
System.out.println(i+" "+record[i]);
}
}
static class Pair{
int index,c,p;
public Pair(int index,int c,int p){
this.index = index;
this.p = p;
this.c = c;
}
}
static class Car{
int index,r;
public Car(int index,int r){
this.index = index;
this.r = r;
}
}
}
|




