双端队列和双向广搜队列

双端队列

介绍

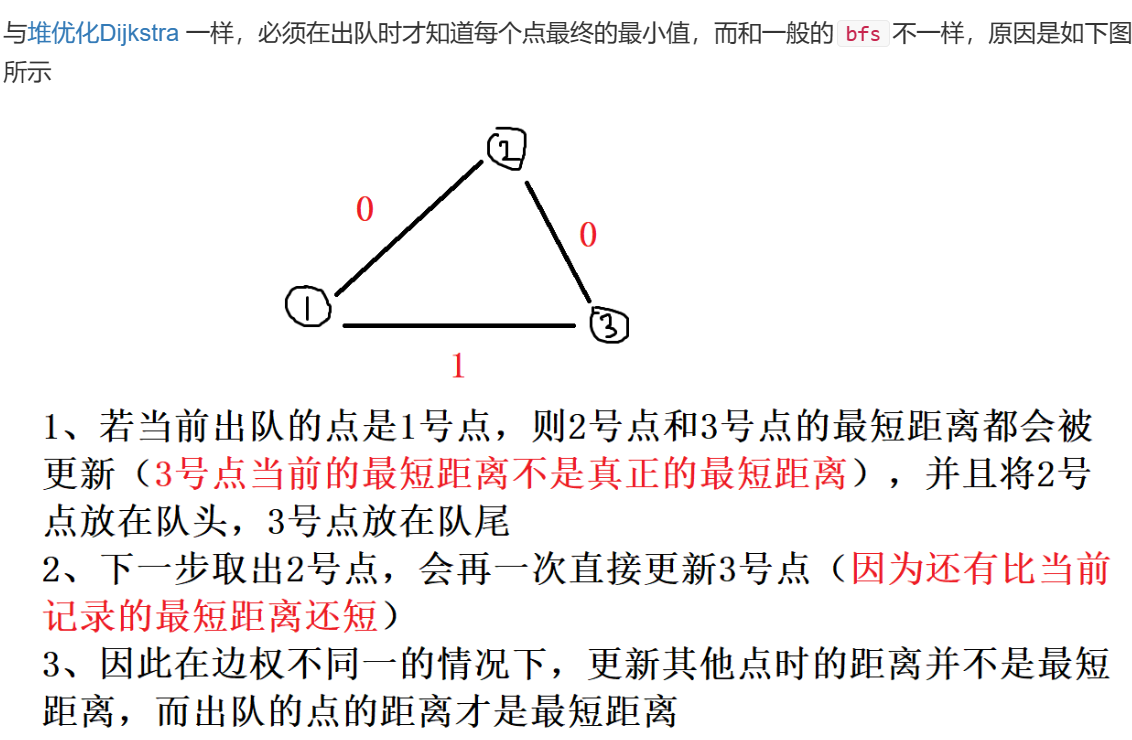
​ 双端队列类似与dijkstra算法，用于求最短路，最短路中权值不是都为1，有1有0的时候可以用到双端队列。每次只要扩展到0那就把点加到对头，每次扩展到1就把点加到队尾。这样来保证bfs维护的队列的两段性和单调性。需要注意的是我们双端队列类似与dijkstra，我们出队的时候判重，因为出队的才是最小的那个距离。

题目

题目概述：

解题思路：
这个题目可以将每个格子的顶点看作是一个点，如果点和点之间有连接，那么它们之间的距离就是0.如果没有链接那距离就是1，所以可以把这个题目总结成图的最短路问题。我们可以用djkstra做也可以用双端bfs做。
双端bfs:
因为题目中存在0和1的边，边不是全都是1，我们如果遍历到0的边那么就往队列开头加，如果遍历到1的边就往队列后加。这样可以保证队列的两端性和单调性。其实就是bfs模拟堆优化版本的dijkstra。
注意：由于我们只能斜线走所以我们只能在x和y方向上做加一减一操作，我们的起点xy之和如果是奇数的话，那么之后只能走奇数点，我们起点是偶数的话那么我们就只能走偶数点。
这个题目需要出队的时候才确认是最小值，才会stu置true。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import java.io.*;
import java.util.*;

class Main{
    public static int N = 510;
    public static char[][] cs = new char[N][N];
    public static boolean[][] stu = new boolean[N][N];
    public static Scanner sc = new Scanner(System.in);

    public static void dfs(int r,int c){
        if((r+c)%2 == 1){
            System.out.println("NO SOLUTION");
            return;
        }
        //代表四个移动方向 分别是 右下，左下，右上，左上
        char[] step = {'\\','/','/','\\'};
        //这个是顶点分别走四个方向的方向向量
        int[] dx = {1,1,-1,-1},dy = {1,-1,1,-1};
        //这个是我们计算四个方向有没有对应的\/的方向向量
        int[] dxs = {0,0,-1,-1},dys = {0,-1,0,-1};
        Deque<Pair> queue = new LinkedList<>();
        queue.addLast(new Pair(1,1,0));
        stu[1][1] = true;
        while(!queue.isEmpty()){
            Pair u = queue.removeFirst();
            int x = u.x,y = u.y,d = u.d;
            stu[x][y] = true;
            if(x == r+1 && y == c+1){
                System.out.println(d);
                break;
            }
            for(int i = 0;i < 4;i++){
                int tx = x + dx[i],ty = y + dy[i];
                //我们的顶点要比r，c分别大一
                if(tx < 1 || ty < 1 || tx > r + 1 || ty > c + 1) continue;
                if(stu[tx][ty]) continue;
                //如果当前方向有边 往队头加
                if(cs[x+dxs[i]][y+dys[i]] == step[i]){
                    queue.addFirst(new Pair(tx,ty,d));
                    
                }
                else{
                    queue.addLast(new Pair(tx,ty,d+1));
                }
            }
        }
    }

    public static void main(String[] args){
        int t = sc.nextInt();
        while((t--)!=0){
            int r = sc.nextInt(),c = sc.nextInt();
            for(int i = 1;i <= r+1;i++){
                Arrays.fill(stu[i],false);
            }
            for(int i = 1;i <= r;i++){
                String s = sc.next();
                for(int j = 1;j <= c;j++){
                    cs[i][j] = s.charAt(j-1);
                }
            }

            dfs(r,c);

        }
    }

    static class Pair{
        int x,y,d;
        public Pair(int x,int y,int d){
            this.x = x;
            this.y = y;
            this.d = d;
        }
    }
}

双向广搜队列

介绍

​ 双向广度优先搜索（Bidirectional Breadth-First Search）算法。这是一种在图或树中寻找最短路径的算法，其特点是从起点和终点同时进行广度优先搜索，直到两个搜索相遇。

以下是双向广度优先搜索的一般步骤：

  1. 初始化：
    • 同时从起点和终点开始两个广度优先搜索。
    • 给起点和终点分别分配一个起始层级（深度）为0的层。
  2. 交替进行搜索：
    • 在每一轮中，从起点和终点分别向外扩展一层。
    • 检查两个搜索的状态是否相遇。如果相遇，说明找到了一条路径。
  3. 判定相遇：
    • 当两个搜索相遇时，可以根据实际需求确定路径的具体形式，例如，连接两个搜索的路径。
  4. 终止条件：
    • 当其中一个搜索到达终点，或者两个搜索相遇时，算法可以终止。

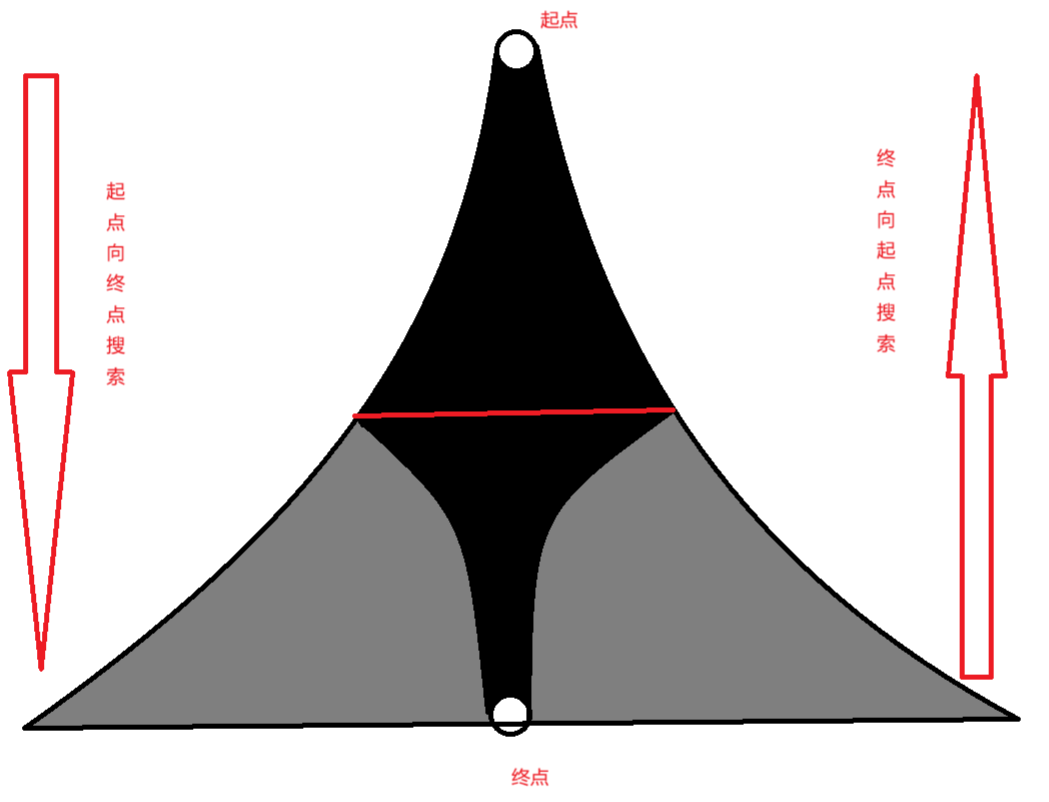
​ 双向广度优先搜索相对于单向广度优先搜索的优势在于，它可以有效地减小搜索空间，提高搜索效率，特别是在寻找最短路径时。它适用于那些有明确起点和终点的问题，例如迷宫求解、图的最短路径等。

​ 如下图所示，灰色空间是我们单向的搜索空间，黑色是我们双向的搜索空间，双向搜索可以大大减少我们的搜索空间。

题目

题目概述

注意

本题如果每次每一边只扩展一个点了，但这样是不正确的。正确做法应该是每次每边扩展完整一层。

反例如下图所示：

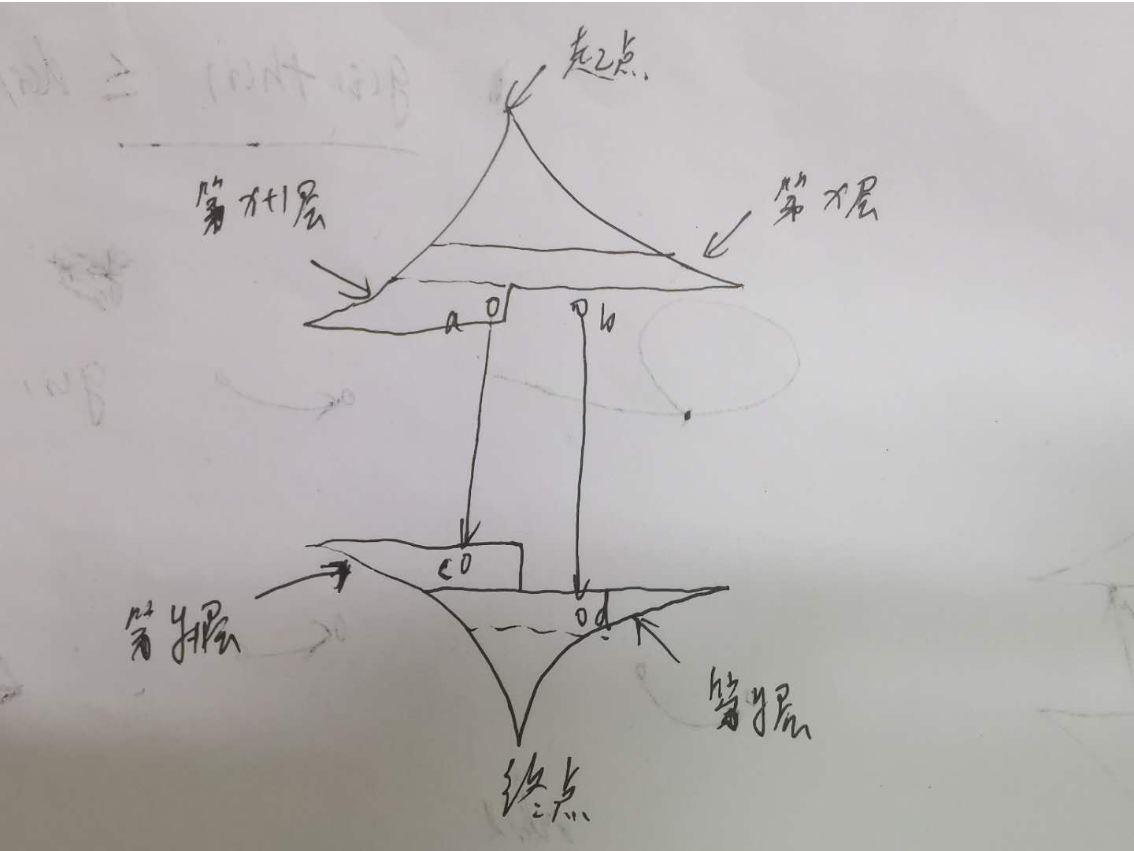
如上图，如果每次不是扩展完整一层，而是只扩展一个点。此时上面该扩展点 a了，点 a 搜到了下半部分的点 c，此时算出的最短路长度是 $$x+1+y+1+1=x+y+3$$但是最优解可能是后面还没扩展到的点 b和点 d之间的路径，这条路径的长度是$$ x+1+y+1=x+y+2$$。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
import java.io.*;
import java.util.*;

class Main{
    public static int N = 10,n;
    public static String[] a = new String[N],b = new String[N];
    public static Scanner sc = new Scanner(System.in);

    public static HashMap<String,Integer> astu = new HashMap<>(),bstu = new HashMap<>(),da = new HashMap<>(),db = new HashMap<>();

    
    
    public static int bfs(String start,String end){
        if(start.equals(end)) return 0;
        Queue<Pair> aqueue = new LinkedList<>(),bqueue = new LinkedList<>();
        aqueue.add(new Pair(start,0));
        astu.put(start,1);
        da.put(start,0);
        bqueue.add(new Pair(end,0));
        bstu.put(end,0);
        db.put(end,0);

        //如果任意一个队列空了 那么就是没有在中间遇见 其实就是没有答案
        while(!aqueue.isEmpty() && !bqueue.isEmpty()){

            //保证两个队列的搜索空间相对平衡 那个空间小就搜索哪一个
            if(aqueue.size() <= bqueue.size()){
                //从起点往终点搜索
                int dd = aqueue.peek().d;

                //开始扩展 注意要一层一层的扩展
                while(!aqueue.isEmpty() && aqueue.peek().d == dd){
                    Pair u = aqueue.remove();
                    String s = u.s;
                    
                    int d = u.d;
                    for(int i = 1;i <= n;i++){
                        for(int j = 0;j < s.length() - a[i].length() + 1;j++){
                            String temp = "";
                            if(s.substring(j,j+a[i].length()).equals(a[i])){
                                temp = s.substring(0,j) + b[i] + s.substring(j+a[i].length(),s.length());
                                if(!astu.containsKey(temp)){
                                    // System.out.println("a:"+s+"-->"+temp);
                                    if(bstu.containsKey(temp)){
                                        //如果另一个方向访问过他
                                        return d+1+db.get(temp);
                                    }
                                    astu.put(temp,1);
                                    aqueue.add(new Pair(temp,d+1));
                                    //记录一下长度
                                    da.put(temp,d+1);
                                }
                            }
                        }
                    }
                }
                
            }else {
                //从终点往起点搜索
                //从起点往终点搜索
                int dd = bqueue.peek().d;

                //开始扩展 注意要一层一层的扩展
                while(!bqueue.isEmpty() && bqueue.peek().d == dd){
                    Pair u = bqueue.remove();
                    String s = u.s;
                    int d = u.d;
    
                    //开始扩展
                    for(int i = 1;i <= n;i++){
                        for(int j = 0;j < s.length() - b[i].length() + 1;j++){
                            String temp = "";
                            if(s.substring(j,j+b[i].length()).equals(b[i])){
                                temp = s.substring(0,j) + a[i] + s.substring(j+b[i].length(),s.length());
                                if(!bstu.containsKey(temp)){
                                    // System.out.println("b:"+s+"-->"+temp);
                                    if(astu.containsKey(temp)){
                                        //如果另一个方向访问过他
                                        return d+1+da.get(temp);
                                    }
                                    bstu.put(temp,1);
                                    bqueue.add(new Pair(temp,d+1));
                                    //记录一下长度
                                    db.put(temp,d+1);
                                }
                            }
                        }
                    }
                }
            }
        }
        return 11;
    }

    public static void main(String[] args) {
        String start = sc.next(),end = sc.next();

        while (sc.hasNext()){
            a[++n] = sc.next();
            b[n] = sc.next();
        }

        int res = bfs(start,end);
        if( res > 10) System.out.println("NO ANSWER!");
        else System.out.println(res);

    }

    static class Pair{
        String s;
        int d;
        public Pair(String s,int d){
            this.s = s;
            this.d = d;
        }
    }
}