A*算法的思路和证明

`A*`算法的思路：

A*算法的目的是优化bfs的搜索空间，如下图所示，我们正常的搜索空间是灰色面积，但是我们的A*算法根据我们的决策，每次选择相对于更加好的决策，优化搜索空间，最后优化的搜索空间更接近与红色面积。

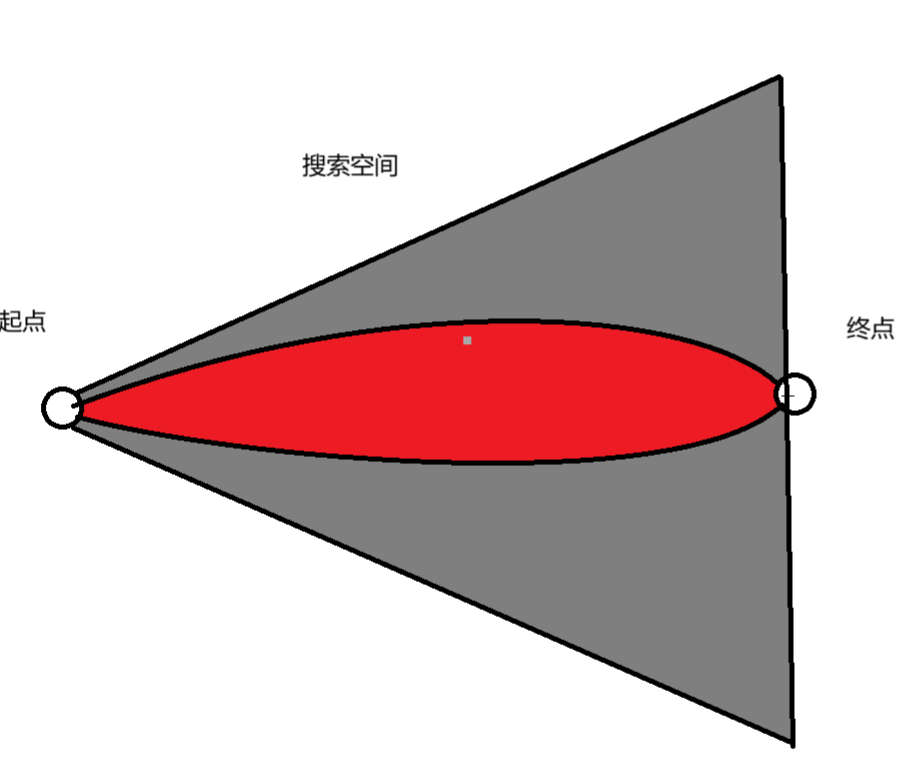
A*算法是针对于所有的非负权边，题目必须有解，不然A*算法的会搜索所有的空间，不如朴素的bfs，因为A*算法维护优先队列，比普通队列多了O(logn)的时间复杂度。

A*算法包含以下几点：

相对于bfs维护的队列不同，A*使用一个优先队列维护从起点s到当前点u的真实距离d(u)和从前点u到终点t预估距离f(u)。
当终点第一次出队的时候break。
dijkstra算法是一种特殊的A*算法，所有的到终点预估距离都是f(u) = 0。
每个点u到终点的预估距离f(u)必须小于等于真实距离g(u)，这样可以保证最后终点出来是最优解。

`A*`的相关证明

为什么我们每个点u到终点的预估距离f(u)必须小于等于真实距离g(u)，这样可以保证最后终点出来是最优解？

假设法：

假设我们终点出队的时候dist并不是最优解$$d_{最优解}$$也就是$$dist > d_{最优解}$$

此时我们的队列中肯定会有一个最优解中的某一个点u存在，并且有$$d(u) + f(u) \le d(u) + g(u) = d_{最优解}$$因此，我们的u满足$$d(u) + f(u) \le d_{最优解}$$因此我们队列头出来的结果dist满足$$d(u) + f(u) < dist$$这个和我们优先队列头dist是最小值矛盾。因此我们驳回原有假设。所以每个点u到终点的预估距离f(u)必须小于等于真实距离g(u)，这样可以保证最后终点出来是最优解。

`A*`深入理解

我们首先假设除了点n1其余所有点的预估函数值f(x) = 0，并且点n1的预估函数等于他相对终点的真实距离L，这个假设满足我们的$$f(x) \le g(x)$$的条件。如下图所示，我们的点已经扩展到n1和n2，因为$$d(n1) + f(n1) < d(n2) + f(n2)$$所以我们会优先扩展n2这条线路。

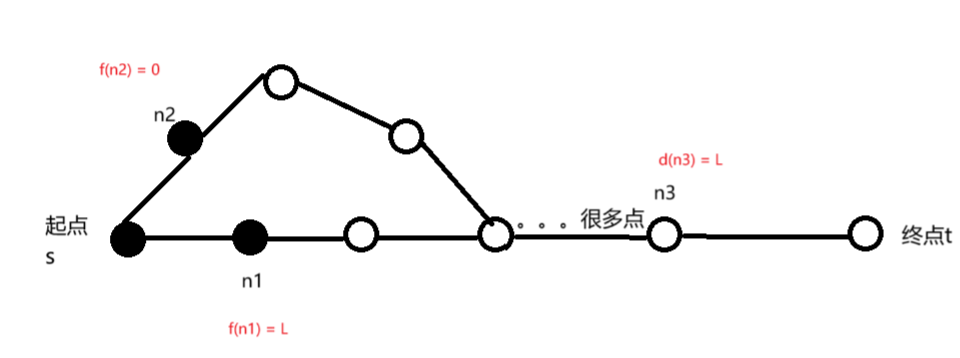
当我们更新到点n4的时候，也就是n4出队的时候，我们存储的值是$$f(n4) + d(n4) = 4$$但是如果我们按照n1线路走的话，也就是按照最优线路走的话，我们得到的值应该是$$d(n4) + f(n4) = 3$$由此可以看出，出队的最小距离只针对终点成立，对其余点都不成立。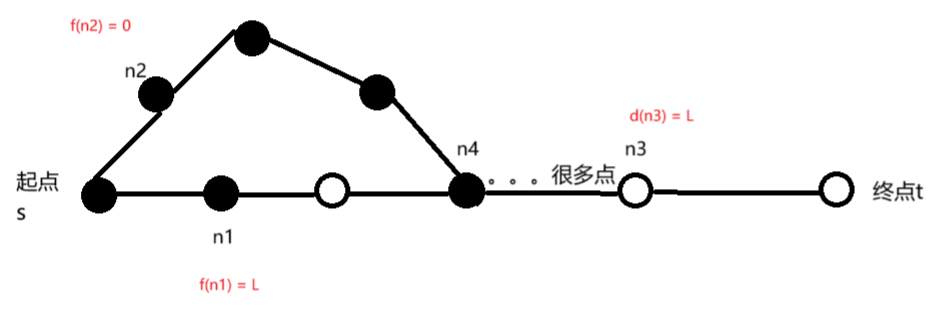

但是我们A*算法是如何拨乱反正的呢？当我们按照n2线路走到n3的时候，我们队列维护的值到了$$d(n3) + f(n3) = L$$这个时候我们会发现队列中最小的点是n1,于是我们就会走n1的道路再走到终点。此时我们会再次经过n4。由此可见我们每一个点出队列之后还是有可能会访问。

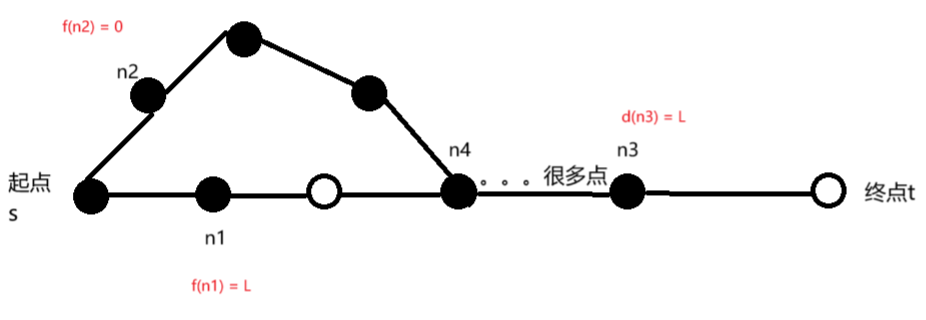
`bfs`,`dijkstra`,`A*`总结

对于bfs，我们每一个点都只会入队一次，所以我们入队判重。
对于dijkstra，我们一旦出队就是最优解，所以我们出队判重。
对于A*，我们除了终点出队是最优解，其余点出队都不是最优解，每一个点出来都更新一次就好了。

相关题目

题目1

注意

我们每个访问到的点之前都可能访问过，如果起点到当前点的距离没有之前访问小，就不用访问了。
我们需要记录下来起点到当前点的距离，并且一直更新。

代码

import java.io.*;
import java.util.*;

class Main{
    public static int[] mhd = {0,0,1,2,1,2,3,2,3,4};
    public static HashMap<String,Integer> stu = new HashMap<>();
    public static Scanner sc = new Scanner(System.in);

    public static int f(String state){
        int res = 0;
        for (int i = 0; i < state.length(); i ++ )
            if (state.charAt(i) != 'x')
            {
                int t = state.charAt(i) - '1';
                res += Math.abs(i / 3 - t / 3) + Math.abs(i % 3 - t % 3);
            }
        return res;
    }


    public static String move(String state,int x1,int y1,int x2,int y2){
        char[] s1 = state.toCharArray();
        int k1 = x1*3+y1,k2 = x2*3+y2;
        char temp = s1[k1];
        s1[k1] = s1[k2];
        s1[k2] = temp;
        return new String(s1);
    }


    public static void bfs(String start){
        int[] dx = {-1,0,1,0},dy = {0,1,0,-1};
        String[] m = {"u","r","d","l"};
        PriorityQueue<Pair> queue = new PriorityQueue<>(new Comparator<Pair>() {
            @Override
            public int compare(Pair o1, Pair o2) {
                return o1.d - o2.d;
            }
        });

        int sx = 0,sy = 0;
        for(int i = 0;i < start.length();i++)
            if(start.charAt(i) == 'x'){
                sx = i / 3;
                sy = i % 3;
            }

        queue.add(new Pair(start,"",f(start),sx,sy));
        stu.put(start,0);
        while(!queue.isEmpty()){
            Pair u = queue.remove();
            int x = u.x,y = u.y,d = u.d;
            String state = u.s,step = u.step;
            if(u.s.equals("12345678x")){
                System.out.println(step);
                return;
            }
            for(int i = 0;i < 4;i++){
                int tx = x + dx[i],ty = y + dy[i];
                if(tx < 0 || ty < 0 || tx > 2 || ty > 2) continue;
                String moveTo = move(state,x,y,tx,ty);
                //如果访问过并且起点到这个点的距离比我们当前还小就不用访问了
                if(stu.containsKey(moveTo) && stu.get(moveTo) <= stu.get(state)+1) continue;
                queue.add(new Pair(moveTo,step+m[i],stu.get(state)+1+f(moveTo),tx,ty));
                stu.put(moveTo,stu.get(state)+1);
            }
        }
    }
    public static void main(String[] args) {
        String start = "";
        while(sc.hasNext()){
            start += sc.next();
        }
        int res = 0;
        for(int i = 0;i < start.length();i++){
            for(int j = i+1;j < start.length();j++){
                char x = start.charAt(i),y = start.charAt(j);
                if( x > y && x != 'x' && y != 'x') res++;
            }
        }

        if(res%2 != 0){
            System.out.println("unsolvable");
            return;
        }
        bfs(start);

    }

    static class Pair{
        String s;
        String step;
        int d,x,y;
        public Pair(String s,String step,int d,int x,int y){
            this.step = step;
            this.s = s;
            this.d = d;
            this.x = x;
            this.y = y;
        }
    }
}

题目2：

题目

思路
这个题目需要求第k短的路径长度，那么我们入队需要把所有的点都扩展，不能因为优化，只如小的点。当我们遍历到第k次终点时，那就是第k短路。同时我们估计当前点到终点的距离，就看做是当前点到终点的最短距离，由dijkstra计算。记住这个时候我们有两个h数组，一个是正向的用作astar一个是逆向的用作dijkstra。
为什么第k个终点就是第k短路？

假设我们第2个出来的终点不是第k短路，由于最短路之前已经出来过了，所以我们队列里面含有一个点u。能满足$$f(u)+d(u) < dk < d(u) + f(u)$$ 这样和我们队列头是最小的矛盾，所以第k个出来的就是第k短路。这个结论对所有的终点有效
代码

import java.io.*;
import java.util.*;

class Main{
    public static int N= 1010,M = 20010,idx,k;
    public static int[] h = new int[N],rh = new int[N],e = new int[M],ne = new int[M],w = new int[M],f = new int[N],d = new int[N];
    public static boolean[] stu = new boolean[N];
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    
    public static void add(int[] h,int a,int b,int x){
        e[idx] = b;
        w[idx] = x;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    
    public static void dijkstra(int start){
        PriorityQueue<Pair> queue = new PriorityQueue<>(new Comparator<Pair>(){
            public int compare(Pair o1,Pair o2){
                return o1.d - o2.d;
            }
            
        });
        queue.add(new Pair(start,0,0));
        f[start] = 0;
        while(!queue.isEmpty()){
            Pair u = queue.remove();
            int x = u.x,d1 = u.d;
            stu[x] = true;
            for(int i = rh[x];i != -1;i = ne[i]){
                int tx = e[i],td = w[i];
                if(!stu[tx] && f[tx] > d1 + td){
                    f[tx] = d1 + td;
                    queue.add(new Pair(tx,f[tx],0));
                }
            }
        }
        
        
    }
    
    public static int astar(int start,int end){
        int cnt = 0;
        PriorityQueue<Pair> queue = new PriorityQueue<>(new Comparator<Pair>(){
            public int compare(Pair o1,Pair o2){
                return o1.d - o2.d;
            }
            
        });
        
        queue.add(new Pair(start,f[start],0));
        while(!queue.isEmpty()){
            Pair u = queue.remove();
            int x = u.x,d = u.d,tr = u.tr;
            if(x == end){
                cnt++;
            }
            if(cnt == k){
                // 
                return d;
            }
            for(int i = h[x];i != -1;i = ne[i]){
                int tx = e[i],tw = w[i];
                if(f[tx] == 0x3f3f3f3f) continue;
                queue.add(new Pair(tx,f[tx]+tw+tr,tw+tr));
            }
        }
        
        return -1;
    }
    
    public static void main(String[] args)throws Exception{
        String[] s1 = br.readLine().split(" ");
        int n = Integer.parseInt(s1[0]),m = Integer.parseInt(s1[1]);
        Arrays.fill(h,-1);
        Arrays.fill(rh,-1);
        Arrays.fill(f,0x3f3f3f3f);
        Arrays.fill(d,0x3f3f3f3f);
        for(int i = 1;i <= m;i++){
            String[] s2 = br.readLine().split(" ");
            int a = Integer.parseInt(s2[0]),b = Integer.parseInt(s2[1]),x = Integer.parseInt(s2[2]);
            add(h,a,b,x);
            add(rh,b,a,x);
        }
        String[] s3 = br.readLine().split(" ");
        int start = Integer.parseInt(s3[0]),end = Integer.parseInt(s3[1]);
        k = Integer.parseInt(s3[2]);
        dijkstra(end);
        if(start == end){
           k++;
        }
        System.out.print(astar(start,end));
    }
    
    static class Pair{
        int x;
        int d;
        int tr;
        public Pair(int x,int d,int tr){
            this.x = x;
            this.d = d;
            this.tr = tr;
        }
    }
}

A*算法的思路和证明